


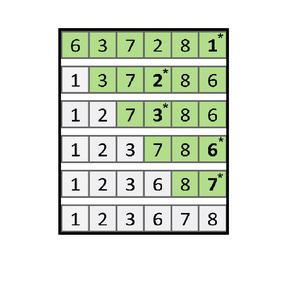
Taking a look at the element with the value of 8, we can see it "bubbling up" from the beginning of the array to its proper place. If it isn't, we swap the elements it consists of. If the pair is in the desired order, we do nothing. Starting from the beginning of the collection we want to be sorted - we compare elements within a pair. The idea behind Bubble Sort is rather simple. Depending on your data type and purpose, the comparison can be done via a relational operator or through a custom comparison function. This means that it compares individual elements within the collection during runtime. Bubble Sortīubble Sort is a comparison-type sorting algorithm. We will also check out its time complexity, and compare it to some other sorting algorithms.Īdditionally, we'll implement one of its variants - Cocktail Shaker Sort in an attempt to optimize it. In this article, we'll explain how Bubble Sort works and implement it in JavaScript. So swap times is the critical bottleneck of the. The compare time and other running time can be ignored. And obviously reading time is less than writing time even in memory. but when using bubble sort, it swaps almost n(n-1). When using selecting sort it swaps n times at most.
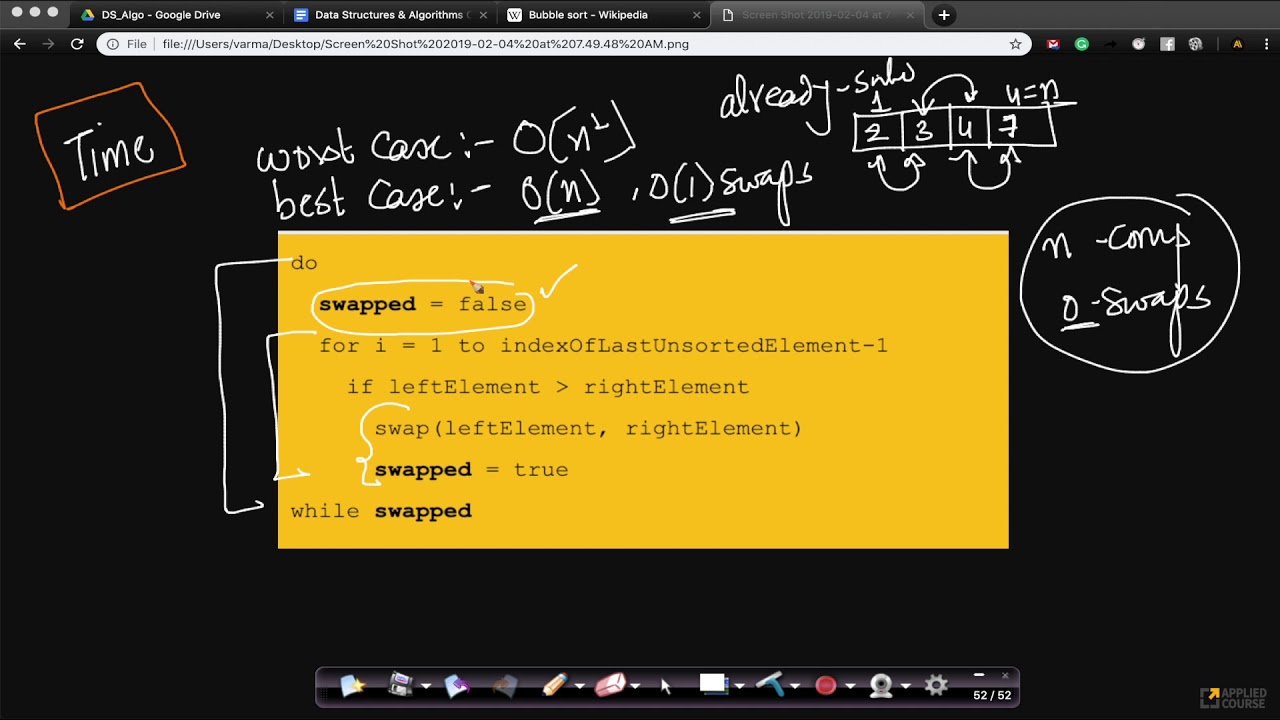
This is why Bubble Sort is used primarily as an educational tool. Bubble sort uses more swap times, while selection sort avoids this. Especially compared to faster, more popular and widely used algorithms like Quicksort or Merge Sort. However, this simple algorithm has shown poor performance in real-life problems. It is usually one of the first sorting algorithms that CS students come across due to its simplicity and the fact that it is quite intuitive and easy to translate into code. The worst-case complexity of Shellsort is therefore connected with the Frobenius problem: for given integers h 1.Bubble Sort, sometimes also referred to as Sinking Sort is one of the most widely known sorting algorithms. Every h 1-sorted and h 2-sorted array is also ( a 1 h 1+ a 2 h 2)-sorted, for any nonnegative integers a 1 and a 2. The following property holds: after h 2-sorting of any h 1-sorted array, the array remains h 1-sorted. If the maximum input size is small, as may occur if Shellsort is used on small subarrays by another recursive sorting algorithm such as quicksort or merge sort, then it is possible to tabulate an optimal sequence for each input size.
gaps = // Ciura gap sequence # Start with the largest gap and work down to a gap of 1 # similar to insertion sort but instead of 1, gap is being used in each step foreach ( gap in gaps ), can be recommended for practical applications. Using Marcin Ciura's gap sequence, with an inner insertion sort. It is an adaptive sorting algorithm in that it executes faster when the input is partially sorted. Shellsort is not stable: it may change the relative order of elements with equal values. In both cases insertion sort works efficiently. The last pass, 1-sorting, is an ordinary insertion sort of the entire array ( a 1., a 12).Īs the example illustrates, the subarrays that Shellsort operates on are initially short later they are longer but almost ordered. The next pass, 3-sorting, performs insertion sort on the three subarrays ( a 1, a 4, a 7, a 10), ( a 2, a 5, a 8, a 11), ( a 3, a 6, a 9, a 12). The first pass, 5-sorting, performs insertion sort on five separate subarrays ( a 1, a 6, a 11), ( a 2, a 7, a 12), ( a 3, a 8), ( a 4, a 9), ( a 5, a 10). In practice the gap sequence could be anything, but the last gap is always 1 to finish the sort (effectively finishing with an ordinary insertion sort).Īn example run of Shellsort with gaps 5, 3 and 1 is shown below. Our second gap ( k) is 256, which breaks the array into four sections (starting at 0,256,512,768), and we make sure the first items in each section are sorted relative to each other, then the second item in each section, and so on. We then run through the list comparing each element in the first half to the element in the second half. In simplistic terms, this means if we have an array of 1024 numbers, our first gap ( h) could be 512. Following this idea for a decreasing sequence of h values ending in 1 is guaranteed to leave a sorted list in the end. If the list is then k-sorted for some smaller integer k, then the list remains h-sorted. Beginning with large values of h allows elements to move long distances in the original list, reducing large amounts of disorder quickly, and leaving less work for smaller h-sort steps to do. It can also be thought of as h interleaved lists, each individually sorted. The idea is to arrange the list of elements so that, starting anywhere, taking every hth element produces a sorted list. Shellsort is an optimization of insertion sort that allows the exchange of items that are far apart.


 0 kommentar(er)
0 kommentar(er)
